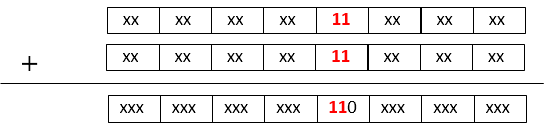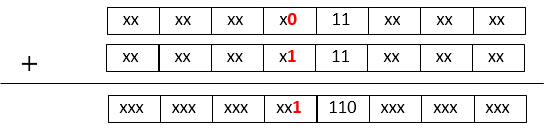CSAについて[1]
- 通常の加算はLSBから計算をした時にCarryを次のビットの加算に加えて計算するので最後のMSBまでCarryが伝搬する可能性がありその分計算時間が遅延します。加算を高速化する方法は以下のように各種存在しますがほとんどが一つの加算を高速化する方法です。(各詳細は割愛します)[2]
- Carry look-ahead adder
- Carry select adder
- Carry skip adder
- Carry save Adder
- Hybrid addr (上記の組み合わせ)
- Carry save adder(以下CSA)は各ビットで発生したCarryを別に保存し次のビットへのCarryの伝搬を抑えることで計算の遅延を少なくするものですが、別々に保存したValueとCarryを元の形に戻す際にCarryの解決をすることになるのであまりメリットがありません。例えばCSAの加算時には各桁2回加算するのでビット数に関係なく遅延は2となりますが、通常の値に戻す際にCarryを解決するためにビット数分の遅延が発生してしまうためです。
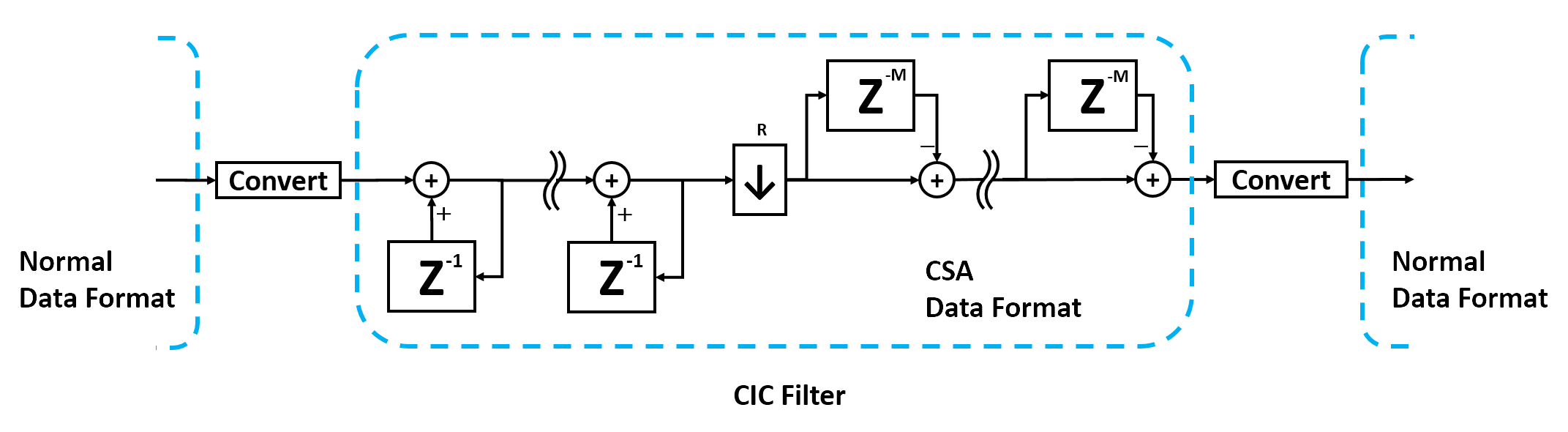
- しかしながら、CICフィルタなどのフィルタ処理において過去の加算結果との加算が連続して行われるような場合はCSAが優位になると考えました。CICフィルタは積分器や微分器をカスケードしたものとなるので、前段から出てきた加算結果を通常の形式に戻すことなくCSA形式のままで演算を行うことが出来れば通常の形式に戻すための遅延が発生することなく高速に処理することが出来るのではないかと言う事です。つまりCICフィルタの最後でだけ通常の形式に戻せば良いのです。
CSAの概要
- 以下にCSAの計算方法について説明します。CSAではCarryが上位に伝播しないように各桁でCarryを持つようにします。つまり各桁でValueとCarryの合わせて2ビット持ちます。
例えば
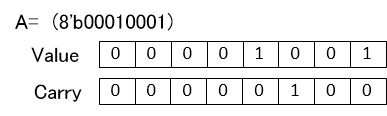
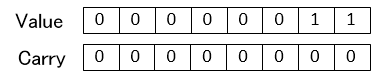
A=8'b00000101
B=8'b00001100
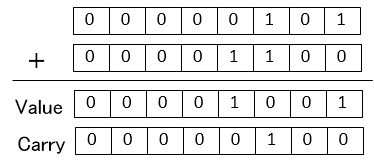
の加算(A+B)をした場合以下のようにValueをCarryに反映しないでそのままCarryとして持っておきます。
このようにCSA形式では数値をValueとCarryで表すします。なおCSA形式での値を通常の数値に戻したい時はCarryを反映させるため以下の様にCarryを左に1シフトしたものとValueを加算します。
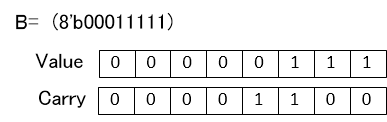
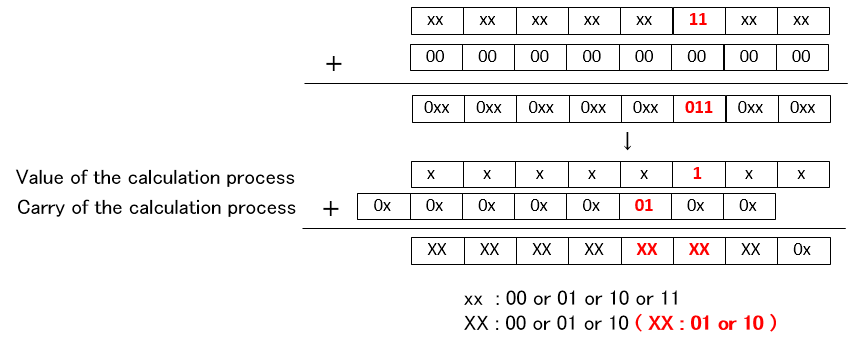
次にCSA形式同士の加算について説明します。まずCSA形式での計算を何度か行った結果Carryにも値が入ったA、Bがあったとします。各桁をValueとCarryでパックされた2ビットづつのデータとします。
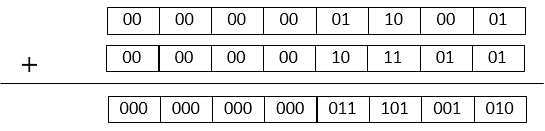
まず最初に各桁を2ビットのデータとして加算して中間の計算結果を出します。2ビットと2ビットの加算結果として途中の計算結果を各桁3ビットにします。
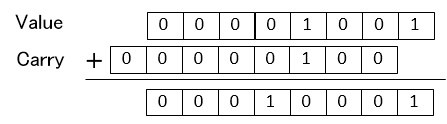
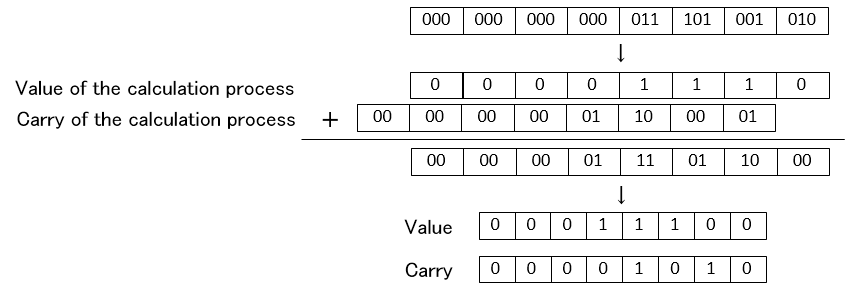
この結果をValueとCarryに整理します。各桁の途中の計算結果上位2ビットは次の桁へのCarryなので、前の桁の上位2ビットとその桁のValueである下位1ビットを以下のように加算します。
つまり1回の加算でCarryの伝播を一度だけ行います。このような方法で通常形式の値を加算してCSA形式にしたり、そのCSA形式の値を加算したりします。
CSAのオーバーフロー問題
- これまで説明してきたようにCSAの加算はValueとCarryに分けた2ビットの加算処理となります。CSA形式で無い値をCSA形式へ変換して計算する場合はCarryが無いためにオーバーフローが発生しませんが、CSA形式同士の計算となるとオーバーフローが発生する可能性があることが分かります。
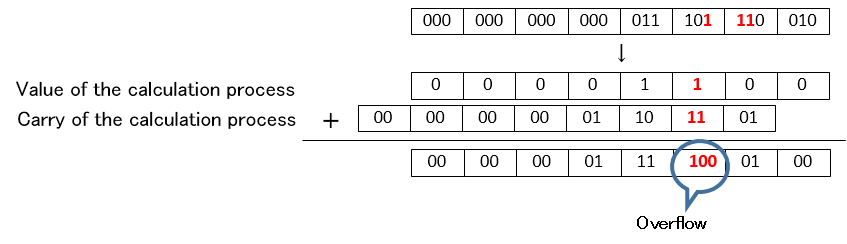
例えば値Aと値Bの各桁のValueとCarryが加算された3ビットが以下のような場合
となり3桁目がオーバーフローしてしまいます。本来ならばこれをもう一つ上位の桁に伝播させる必要があります。しかしながらこれを伝播させていてはCSAのメリットが薄れてしまいます。
オーバーフローした場所をみるとxx1 11xとなってしまう時に発生することがわかります。これは加算する値AとBにおいて以下の条件が成り立つときに発生します。
- AとBの桁NがValueとCarry共に1の時
- AとBのどちらかの桁N+1がValueが1でもう一方が0の時
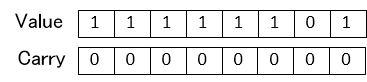
1.と2.の条件が重ならないようにする方法がないかを考えてみます。CSA形式では同じ値でも以下のように表現がいくつか存在します。(どれも同じ値 8'b00010011)
当然Carryがすべて0の場合には問題ありませんがそれはCarryをすべて解決することになるので通常形式に戻すのと同じことになってしまいます。Carryを全て解決することなくオーバーフローしない条件の表現を作り出せないかを検討しました。値を変えずにCarryの伝播をもう一度だけすればオーバーフロー条件を回避できるかを見てみます。つまり0を加算してみます。以下の様に条件の1.となっている値に0を加算してみます。
結果はValueとCarryの両方が1にならないため条件1.をクリアすることが分かります。このことからCSAで出てきた結果に0を加算することでオーバーフローを回避できます。余分に加算するようですが全ての桁にCarryが伝播する可能性のある通常の加算よりは速度的にもましであると考えます。
CSAによる減算
- 次に減算について考えます。先に述べたCICフィルタの微分モジュールでは減算が必要となります。通常減算は2の補数の加算で行います。
例えば
8'b00001000 − 8'b00000011 = 8'b00000101
を例にします。2の補数とは 2^N bit - 値 です。
9'b100000000 − 8'b00000011 = 8'b11111101
つまり、反転して+1となります。上記の減算を2の補数で加算することで計算すると
8'b00001000 + 8'b11111101 = 8'b00000101
- ここで8'b00000011をCSAで表すと
2の補数8'b11111101をCSAで表すと
となりValueとCarryを反転してValueとCarryに共に+1した値であることが分かります。CSA形式はValueとCarryがパックされたものとしているためValueとCarryを一緒に反転出来るほうが都合が良いと言えます。
- 例として
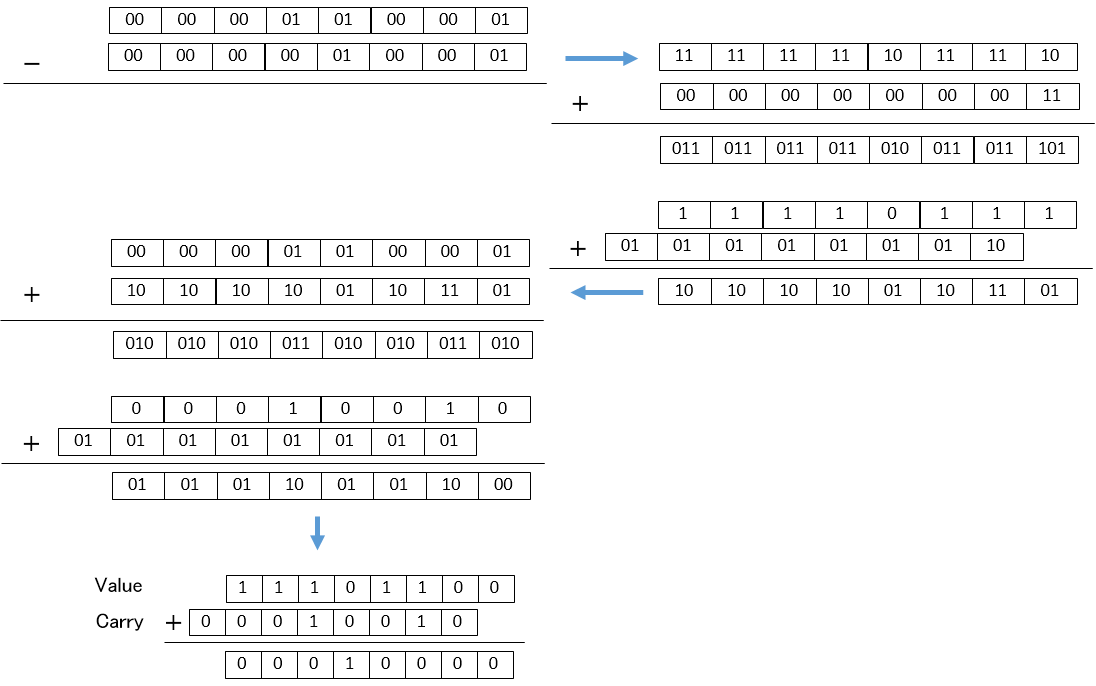
8'b00011001 − 8'b00001001 = 8'b00010000
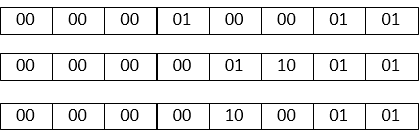
を計算します。CSA形式にして計算すると
となり、このことから減算もCSA形式のまま行うことが出来る事が分かります。[3]
CSAコード
/* **************************** MODULE PREAMBLE ********************************
Copyright (c) 2012, ArchiTek
This document constitutes confidential and proprietary information
of ArchiTek. All rights reserved.
*/
// ***************************** MODULE HEADER *********************************
//
// 通常形式の値とCSA形式の値を足すためのmodule
// CSA形式の値+通常の値=CSA形式の値
//
module CSA (
iA,
iB,
oY
);
// ************************ PARAMETER DECLARATIONS *****************************
parameter W = 4; // 通常形式のビット幅
// *************************** I/O DECLARATIONS ********************************
// Input
input [W*2-1:0] iA; // CSA形式の入力値 A
// ビット幅は通常形式の2倍
input [W-1:0] iB; // 通常形式の入力値 B
// Output
output [W*2-1:0] oY; // CSA形式の出力値
// ビット幅は通常形式の2倍
// ************************** LOCAL DECLARATIONS *******************************
// ****************************** MODULE BODY **********************************
//実際の処理はCSAFuncで行う
assign oY = CSAFunc(iA, iB);
// ************************** FUNCTIONS and TASKS ******************************
function [W*2-1:0] CSAFunc;
input [W*2-1:0] opA;
input [W-1:0] opB;
reg [1:0] result[0:W-1];
reg [1:0] tmp;
integer i;
begin
// 0ビット目の加算結果をresultに入れる
// 0bit目はCarryはない
result[0] = {1'd0, opA[0]}
+ {1'd0, opB[0]};
// 1ビット目以降の加算結果をresultに入れる
// 1ビット目以降は一つ前のCarryと値AとBのValueを加算
for (i=1; i < W; i=i+1)
result[i] = {1'd0, opA[i*2-1]}
+ {1'd0, opA[i*2]}
+ {1'd0, opB[i]};
// resultをCSA形式に詰めなおす
for (i=0; i < W; i=i+1) begin
tmp = result[i];
CSAFunc[i*2+1] = tmp[1];
CSAFunc[i*2] = tmp[0];
end
end
endfunction
endmodule
// *****************************************************************************
CSA形式 ⇔ 通常形式 変換コード
- 通常の値をCSAへ変換して計算する場合や、CSA形式の結果を通常の形式に戻す場合以下のfunctionを組み込んで使用します。
//
// 通常の値をCSA形式に変換するfunction
//
function [CSA_BIT_W-1:0] bin2csaFunc;
input [BIT_W-1:0] data;
integer i;
begin
for(i=0 ; i < BIT_W ; i=i+1) begin
bin2csaFunc[i*2] = data[i]; // Value部分に値を入れる
bin2csaFunc[i*2+1] = 1'b0; // Carry部分には0を入れる
end
end
endfunction
//
// CSA形式の値を通常の値に変換するfunction
//
function [BIT_W-1:0] csa2binFunc;
input [CSA_BIT_W-1:0] data;
reg [BIT_W-1:0] carry;
reg [BIT_W-1:0] value;
integer i;
begin
for (i=0; i < BIT_W; i=i+1) begin
carry[i] = data[i*2+1]; // Carry部分を取り出す
value[i] = data[i*2]; // Value部分を取り出す
end
// Carry部分を左に1bitシフトしてValueと足す
csa2binFunc = {carry[BIT_W-2:0], 1'b0} + value;
end
endfunction
回路デザイン > テクニック > 高速演算 次のページ(パイプラインフィードバック) このページのTOP ▲