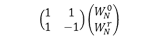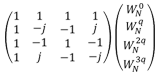目的

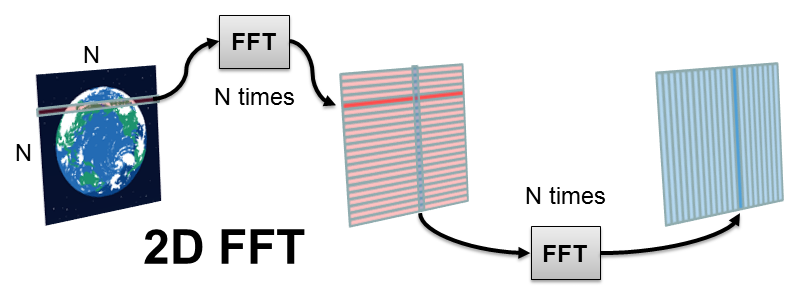
離散フーリエ変換（DFT）は周波数解析等で非常に役に立つことは周知の通りです。FFTはDFTの計算を高速化した変換方式で、さまざまな文献で述べられています。ここでは、このFFTのハードウェア化について述べます。原理は各方面で述べられているので割愛します。

近年、CPUやGPUの高速化に伴って、特別なハードを用いなくてもある程度のことはできるようになってきました。しかし、画像解析など2Dや3Dの走査が必要な場合もあり、FFTのハードウェア化要望はこれからも続くと思われます。従って、ハードウェア化に際しCPUやGPUの性能を大きく越える^[1]ことが目標になります。

ここまで半精度の浮動小数点を説明してきたこともあって、ビット精度が比較的低い画像への適応^[2]を考えます。もちろん、アーキテクチャ的には単精度であっても問題がないように考えます。また性能目標は、XGA相当の画像に対し1画素/サイクル程度を考えます（1D走査）。

実装方式の比較と選択

全サンプル数を一挙に算出するようなハードウェアはコスト上設計困難です。従って、逐次処理を行うことになります。逐次処理の単位はハードウェア設計上、2のべき乗が適しています。特にRadix-2とRadix-4は回転因子の計算する特性上、効率がいいことが分かっています。単位当たりの逐次処理は、パイプライン処理を用いて1サイクルで実施することにします。

逐次処理なので同じ計算機を使い回すことから、様々な条件を網羅する機能が必要になります。逆に、初段は加算が必要ないなど特殊なケースは考えなくてよくなります。

これらのFFTのハードウェア化自体、様々な文献で語られているので、単刀直入に以下のことを検討します。

Radix-2とRadix-4方式の比較

メモリアクセスと扱えるサンプル数

入出力方法

性能はパイプライン化を前提にすると、単位処理（Radix-2/4）あたりの最短処理時間は1サイクルになります。これをN=2ⁿ点FFTに当てはめた場合の性能を見積もります。また、FFTの構成要素は主に演算器になるため、演算器の使用数でコスト^[3][4]を見積もります。具体的に、どのように使っているかはコードを見てください。

方式概略図計算式性能(サンプル当り) コスト(演算器数)

Radix-2 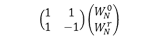1/2 x n 10

Radix-4 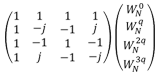1/8 x n 34

上記の表をみると単位処理の効率はRadix-4が優れいていることが分かります。例えば同じ性能を出すために、Radix-2を並列に使うよりもRadix-4を使った方がいいと言うことになります。ここでは、Radix-4を選択^[6]します。N=1024だと1280サイクル必要で、1.25サンプル/サイクルの処理性能になります（目標に近い値）。

次にメモリアクセスに関して考えます。単位処理を同時処理するには入出力ポート分のメモリアクセスが発生します。ここで悩むのが、SRAM等の専用メモリを用いるか、主記憶等の共有メモリを使うかの選択です。ここでは、性能重視のポリシー^[7]に合わせSRAMを用いることにします。

専用メモリ：性能保証と性能最大化が可能、実装容量が有限なので処理可能なポイントは制限

共有メモリ：性能ゆらぎの発生とポートの扱いに制限（複雑化）、任意ポイントの処理が可能

入出力方法ですが、SRAMを使うには入力信号を一旦Loadし、結果を読みだして出力することになります。この期間中にRadxi-4を使用したハードウェアがSRAMを使えないと、性能に多大な影響を与えてしまいます。そこで、入出力とFFTの処理を同時に行うため、SRAMはダブルバッファにする必要があります。これに関しては次の節で述べます。

最後に、詳細は述べませんが付属的な検討事項を上げておきます。必須ではありません。

入出力はパイプライン形式でなく、外部メモリに対して自動で入出力

入出力フォーマット（実数と虚数のパッキング形式、整数型の変換）

2の累乗でない数のデータ、および実数か虚数の0入力を省略したい場合の0埋め処理

逆変換、DCT（その他直交変換）への応用（FCT）

DC成分の正規化

制御のポイント

Radix-4の処理は、計算式通りに組むだけなので難しくありません。ポイントになるのは、性能を最大限にするためのSRAMの扱い方です。Radix-4の処理は、N/4回の一連の処理（Phaseとする）をlog₄N回繰り返します。PhaseごとにSRAMアクセスのパターンが変化しても問題がないようにします。

先ず、SRAMのアクセスに対し以下の条件が導き出せます。

4ポート同時にアクセスできなければならない
→ポートのアドレッシングはPhaseにより異なるため固めることができず、4BankのSRAMが必要

Radix-4の入力と出力分、同時にR/Wを行わなければならない
→R/W同時アクセスのため2ポートSRAMが必要
→上書き防止のためReadとWriteのアドレッシングが排他的になる容量を用意

次に、下記に64点FFT処理における時間対データアドレスの図を示します。入力サンプルは予めデータアドレスのBit Reverseにより並び替えられているものとします（Decimation in timeを採用）。同一サイクルにおいて、4つ黒のBoxがRadix-4の処理になります。

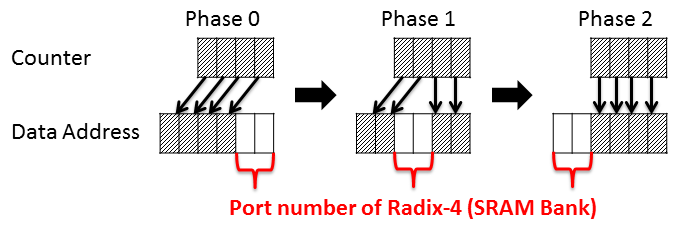
無条件にN/4個をカウントする変数を仮定すると、カウンタとデータアドレスはPhaseごとに以下のようにアドレス配置が変化します（N=64）。Radix-4のポート番号は0,1,2,3が割り当てられます。

ところが、単純にデータアドレスの上位4ビットをSRAMアドレスに、下位2ビットをSRAMのBank番号にすると、時間対データアドレスの図で示すように同一BankのSRAMにアクセスが集中することになります。図において、Phase0では異なる色（異なるBank）、Phase1では同一色（同一Bank）がそれを表しています。

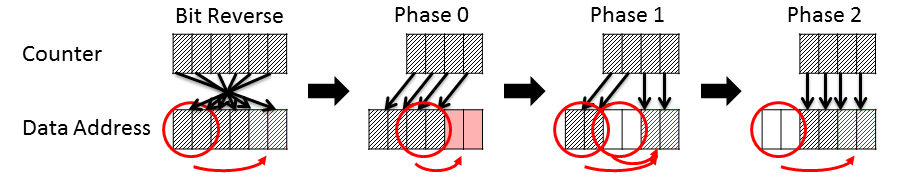
これを回避するため、出力時のBank番号を下位2ビットに対して排他的論理和し、最終的なSRAMアドレスとします。Bank番号により攪拌することで、アドレスの下位2ビット即ちSRAM Bank番号は必ず異なります。また、攪拌の影響が累積しないよう、前回攪拌した部分は再度攪拌し打消すことが必要です。詳しくは述べませんが、Bit Reverse後の入力時と出力時も同じ考えでSRAMアドレスを算出します。

参考に、16点FFTの各Phaseごとのメモリアドレスの変化を示します（ビットアサインがイメージできるよう16進数表記）。入力データはBit Reverseと攪拌によりバラバラにSRAMに格納されます。次にPhase0で順に4つづつ、Phase1で4つ飛びに4つづつSRAMをアクセスします。SRAMアドレスのそれぞれはユニークで、またSRAM Bankのマッピングに使用するLSB2ビットが必ず排他的な関係になっていることが分かります。

元のデータアドレス Bit Reverse SRAM Write Phase 0 Phase 1

0 0 0 0 0

1 8 A 1 5

2 4 5 2 A

3 C F 3 F

4 2 2 5 1

5 A 8 4 4

6 6 7 7 B

7 E D 6 E

8 1 1 A 2

9 9 B B 7

A 5 4 8 8

B D E 9 D

C 3 3 F 3

D B 9 E 6

E 7 6 D 9

F F C C C

もう一つの問題は、SRAMに書き込んだ値を再使用する場合、矢印のGAPのように書き込みと読み込みの時間差が少なく、Radix-4の演算パイプラインのレイテンシを下回る場合です。これは誤って書き込む前のデータを使ってしまい誤計算することを意味します。残念ながら、データアドレスのビットアサインを組み替えても避けようがありません。発生個所が限られているため、特定のPhaseの切り替わり時に演算を止めることにより回避します（パイプライン長が10程度なら64点FFT以下の特定Phaseに限定可能）。

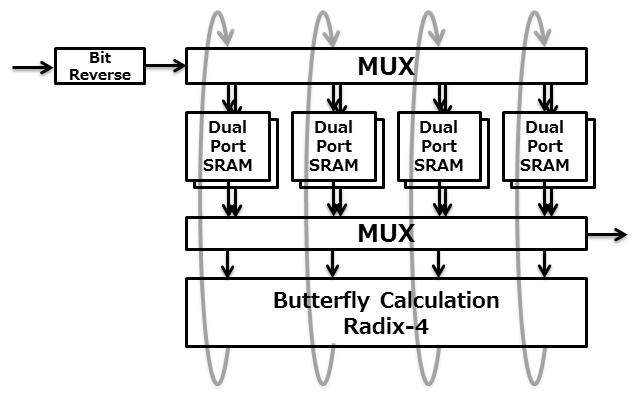
最後に、データの入出力時とデータ加工時の2つの同時アクセスを実行しなければなりません。Radix-4の演算はReadとWriteの2つのポートを占有し、データ入力のためのWriteポートとデータ出力のためのReadポートを加えると、合計4ポートのSRAMが必要になりますが現実的でありません。従って、2ポートSRAMが2セット必要です。上記の4Bankを併せて考えると、8つのSRAMが必要になります。これらを表したのが下の図です。