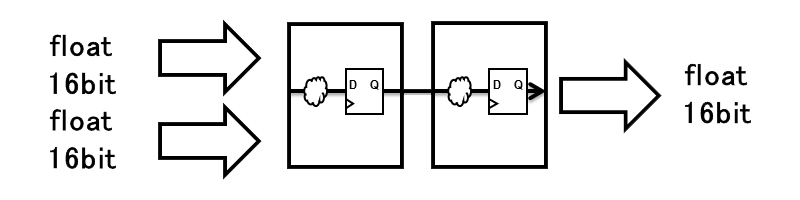浮動小数点を扱うに当たって
- 浮動小数点のメリットは、何と言っても扱う表現できる数値のダイナミックレンジが広いことです。演算過程での桁落ちや飽和のほとんどを考えなくてもよくなります。
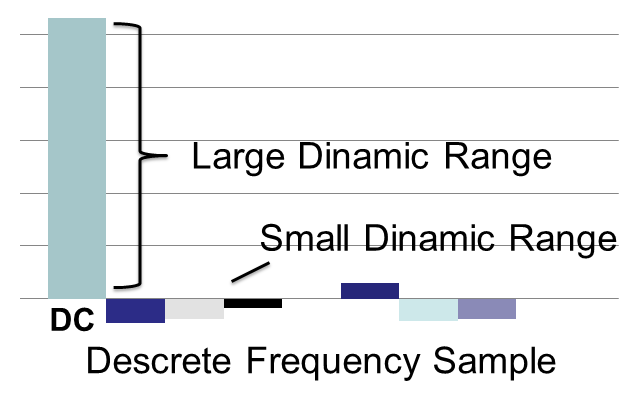
- 例えば画像の離散フーリエ変換を考えましょう。直流成分(周波数0の波)は、全ての画素値の合計で大きな数値になります[1]。一方、交流成分は桁の小さな数値なります。
- これを決まった語長の固定小数点でカバーするには、入出力値や演算過程での精度の持続を考慮しなくてはなりません。直流成分だけ語長を拡大するなど演算ごとの特殊化も考えられます。
- 以上のように浮動小数点は使い勝手がよいのですが、コスト高[2]になるデメリットがあります。固定小数点に見られる最適コストのための語長調整の余地もありません。
- コスト高の要因は、演算自体を除けば演算ごとに生じるまるめと正規化にあります。特に加算に対するコストは高く、扱う語長にもよりますが意外にも加算器と乗算器のコストはそんなに変わりません。
- このようなメリットとデメリットを勘案しながら、一方では固定小数点を、一方では浮動小数点をシステムに適応することになります。三角関数の生成に便利なCORDIC(Coodinate Rotation Digital Computer)の実装では、固定小数点と浮動小数点の中間の処理が必要だったりします。
- さて、浮動小数点のフォーマットはIEEE754で定められたものが一般的に用いられています。今回はパイプライン・プリミティブとして一部の実装を簡単に述べます。
実装の考え方
- 近年、コンシューマーレベルの画像処理でも浮動小数点を使う時代になってきました。そこで、目的を直感的にわかりやすい画像処理の部品作成に定めたいと思います。
- 画像処理は大量のデータ処理になるので、使用する部品をできるだけ小さくして並列に使うことが多くなります。浮動小数点には規約があるので、規約を守りつつダイナミックに小さくできるのかと言うことになります。
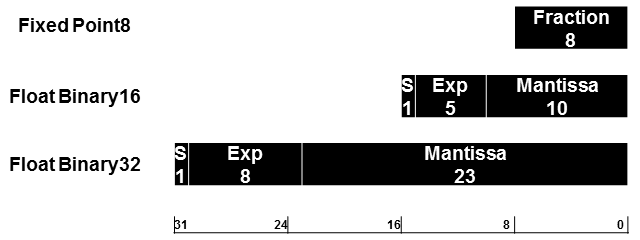
- 画素の要素をRGBとし値が一般的に10bitまでと割り切ると、単精度までの精度は必要ありません。思い切って半精度を採用します。半精度は、最大11bitの精度を持ちます。また、不要な規約をカットすることも検討します。
- 周波数ターゲットは特に定めません。ただし、画素のαブレンド(8bit乗算と加算)を1サイクルで実施する回路を指標にします。つまり、αブレンド回路の論理段数や遅延と同程度になることを目指します(単純なパイプライン構造が期待できるので、FF間の遅延の揺らぎは少ないので当てはめやすい)。
実装の仕様
- 浮動小数点加算器(FAdd)と乗算器(FMul)を設計します。ともに2項演算です。とりあえず簡単な乗算器に関して述べて行きたいと思います。
- 画像等のダイナミックレンジをカバーしつつ比較的コストが安くレイテンシも少ないIEEE Binary16を対象にします。
- NaN(非数)やInfinity(無限大)および非正規化数はサポートしません(途中言及はします)。実際NaNやInfinityは、入出力のダイナミックレンジが確定できれば不要です。非正規化数は、固定小数点を簡単変換して表すことができるので大変便利ですが、今回は割愛します。
- 11bit語長の加算および乗算を1サイクルでするものとし、最終的なレイテンシは2、スループットは1演算/サイクルとします。なお、単精度を扱う場合は、加算器・乗算器ともステージをさらに分けないと遅延設計が大変です(システムクロックに依存します)。
- バッファ型のパイプライン仕様とします。なお、Valid/Stallを既に別系統で実装してあることがあります。この場合、論理合成ツールで重なった論理は消えるものとして二重に実装を許してしまうか、1つに集約しそれぞれに必要なValid/Stallを分配します。ここでは前者とし、そのままValid/Stallの論理を実装します[3]。
- 精度に関して、演算結果の0捨1入を行います。本来は、最近接まるめ(偶数)と言って、丁度1/2の誤差が発生すれば偶数側にまるめます。
回路デザイン > 設計例 [浮動小数点] > 加算・乗算について 次のページ(実装にあたって) このページのTOP ▲